Quand on parle de sciences, on s’intéresse plus souvent aux résultats qu’à la façon dont on les a obtenus. Les outils qui font le lien entre les hypothèses de départ et la conclusion restent le plus souvent dans l’ombre. Et pourtant, sans ces outils, les modèles, la connaissance scientifique serait impossible à atteindre ! Alors qu’est-ce qu'un modèle scientifique ? Pourquoi est-ce qu’on a besoin des modèles en sciences, et en particulier en écologie ? Et est-ce que les modèles représentent la réalité ? C’est ce qu’on vous propose de découvrir dans cet article !
C’est difficile de donner une définition générale des modèles, car ils ont été construits dans différentes disciplines pour répondre à des problèmes particuliers [2, 7]. Dans tous les cas, les modèles sont toujours des outils, c’est-à-dire qu’ils servent à atteindre un but extérieur au modèle lui-même, pour obtenir une meilleure représentation du phénomène auquel on s’intéresse [5, 7].
Les modèles peuvent prendre des formes très variées et ont beaucoup d'utilités différentes. Pour avoir une meilleure idée de ce qu’est un modèle, voici trois exemples de modèles et de leurs applications.
Les organismes modèles sont des espèces dont le fonctionnement est bien connu par les biologistes, comme la souris ou la mouche du vinaigre. Ces espèces permettent de mieux comprendre le fonctionnement des organismes vivants. Par exemple, on peut tester l'efficacité d’un médicament sur des souris : comme cette espèce est assez proche de l’humain, les résultats donneront des indices sur ce à quoi on peut s’attendre pour l'humain.
Les objets abstraits sont des modèles qui permettent d’imaginer une représentation fictive d’un objet réel. Par exemple, le modèle de l’atome permet aux physiciens d’imaginer à quoi ressemble un atome, qu’on ne peut pas le voir directement. Il y a eu plusieurs modèles de l’atome dans l’histoire des sciences, parfois en concurrence. Par exemple, le modèle créé par Ernest Rutherford en 1911 imagine un atome composé d’un noyau autour duquel tournent des électrons [10]. Les modèles de l’atome permettent de mieux comprendre ce qu’est la matière, mais ont aussi des applications concrètes. Par exemple, une extension du modèle de l'atome de Rutherford permet de calculer la longueur d'onde d’un rayonnement émis par des atomes. Ce principe est utilisé par exemple pour concevoir des lasers.
Les modèles mathématiques sont des modèles abstraits qui s’écrivent en langage mathématique. Par exemple, le modèle linéaire permet de calculer la valeur d’une variable y en fonction d’une autre variable x : il s’écrit y = ax + b (où a et b ont des valeurs constantes). Les variables y et x peuvent représenter n’importe quelles grandeurs numériques, et le modèle linéaire a donc beaucoup d’applications. Par exemple, ce modèle est utilisé en mécanique pour calculer la déformation initiale d’un matériau en fonction de la force qu’on lui applique [9]. On l'utilise aussi pour étudier la façon dont la taille est corrélée entre des parents et leurs enfants [11], l’évolution de la température de l’atmosphère au cours des années (en complément d’autres techniques) [6]...
Enfin, les modèles sont utilisés dans différents domaines en sciences, mais ils font eux-mêmes l’objet de recherches. Il y a donc des scientifiques qui travaillent à perfectionner des modèles existants ou à en développer de nouveaux. Par exemple, l’intelligence artificielle est un domaine de recherche actif qui développe des modèles pour réaliser des tâches qui essaient d’imiter une intelligence humaine, telles que comprendre des instructions orales (Siri, Alexa, l’assistant Google...)
Dans la vie de tous les jours, on peut se fier à notre intuition ou à une connaissance partielle pour prendre des décisions. Par exemple, lorsque vous descendez les escaliers, vous ne vérifiez pas la hauteur de chaque marche : ça prendrait beaucoup trop de temps, et on se doute que l’architecte ne s’est pas amusé à faire des marches de hauteurs différentes [5] !
Mais en sciences, on ne peut pas se permettre de faire reposer notre analyse sur ce qui nous semble “évident” si on veut atteindre un niveau de connaissance fiable [5]. L’inconvénient, c’est que c’est beaucoup plus lent d’utiliser un raisonnement logique qu’un raisonnement intuitif [3]. Mais pour produire des résultats fiables, les sciences doivent utiliser cette démarche. Les modèles sont donc des outils pour remplacer notre raisonnement intuitif par un raisonnement contrôlé.
Chaque discipline scientifique a des types de modèles préférés, en raison des contraintes propres au domaine et de la culture de la discipline. Cet article va s’intéresser plus particulièrement au domaine dans lequel je réalise ma thèse : l’écologie, qui est l’étude des relations entre les espèces vivantes et avec leur environnement.
En écologie, on utilise beaucoup les modèles mathématiques [8], comme le modèle linéaire décrit plus haut. En effet, ce type de modèles semble adapté pour décrire un certain nombre de phénomènes en écologie [1]. Par exemple, on utilise des équations différentielles pour prédire la croissance des populations, des modèles statistiques pour connaître l’effectif des populations dans leur milieu naturel, des fonctions mathématiques pour prédire la répartition des espèces en fonction de leur environnement...
Bon à savoir : les modèles mathématiques sont très utilisées en écologie et dans certaines disciplines scientifiques (physique, économie, biologie). Mais les correspondance entre le langage dépouillé des mathématiques et la complexité de la réalité n'est pas une évidence. D'ailleurs les mathématiques ne sont pas utilisées aussi couramment dans d'autres domaines (histoire, littérature).
On va détailler un exemple pour avoir une idée de la logique utilisée pour modéliser des systèmes écologiques. Dans cet exemple, on va s’intéresser à la façon dont les zèbres choisissent leur habitat, c’est-à-dire les zones qu’ils préfèrent dans la savane.
On fait l’hypothèse que les zèbres préfèrent les zones proches des points d’eau. En effet, on a observé sur le terrain qu’ils s’éloignaient peu des points d’eau. De plus, on sait que la savane est un écosystème très rude, avec une saison sèche qui dure la moitié de l’année. Or, les zèbres ont besoin de boire régulièrement. On peut donc penser que l’eau sera une ressource très importante pour eux.
Pour tester cette hypothèse, on peut utiliser un modèle mathématique. Il faut donc choisir une fonction qui décrit la variation de probabilité de présence des zèbres avec la distance à l’eau (voir graphique ci-dessous). Pour choisir cette fonction, on peut s'inspirer de ce qu'on observe dans les données. Par exemple, la fréquence des zèbres en fonction de la distance à l'eau peut diminuer de façon constante, suivre un plateau puis chuter brusquement... Selon ce qui est observé, on utilisera des fonctions mathématiques différentes.
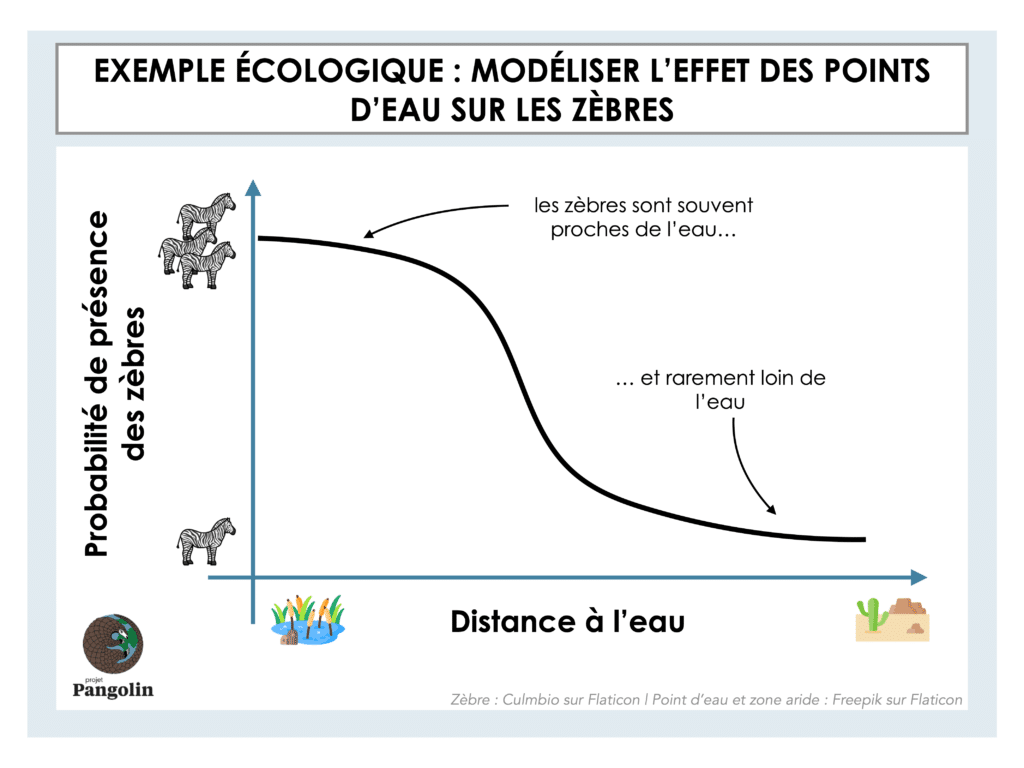
Maintenant qu’on a choisi une fonction pour modéliser notre hypothèse, on doit l’ajuster à notre problème. C’est-à-dire que si notre fonction mathématique s’écrit par exemple probabilité de présence du zèbre = a × exp(-b × distance à l’eau)), on doit déterminer les valeurs des paramètres a et b. L'une des façons de trouver ces paramètres est d'utiliser des programmes informatiques. Par exemple, si on se base sur des données de présence de zèbres à des endroits plus ou moins éloignés des points d’eau, ces programmes vont choisir les paramètres qui réduisent le plus possible l’écart entre la probabilité de présence des zèbres calculée avec le modèle et la fréquence des zèbres observée dans les données.
Pour savoir si le modèle qu’on a finalement choisi décrit bien la réalité, on compare ses prédictions aux données observées. À cette étape, on s’attend à ce que les données soient un peu éloignées des prédictions. En effet, certaines variables ne sont pas prises en compte dans le modèle (comme par exemple la présence des prédateurs). Or, ce qui nous intéresse, c’est de savoir si l’effet de la distance à l’eau est bien décrit : mais comment faire la différence entre un écart au modèle dû à une mauvaise description de l’effet de l’eau ou à d’autres facteurs ? C’est là que les statistiques entrent en jeu : elles permettent de prendre en compte l'écart entre le modèle et les données dû à d’autres facteurs que l'eau. On va donc comparer notre modèle aux données avec une certaine marge d’erreur (c’est le fameux intervalle de confiance statistique) pour prendre en compte ces facteurs non modélisés.
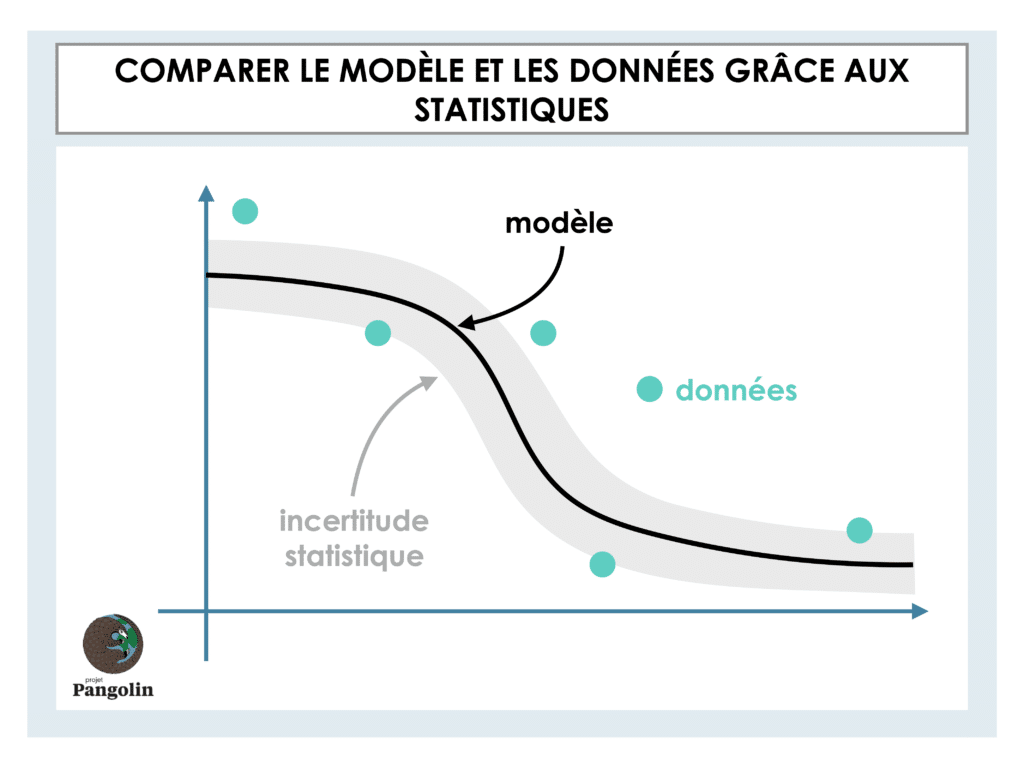
Enfin, malgré tous nos efforts pour construire un bon modèle, on peut parfois se rendre compte qu'il correspond assez mal aux données observées. Dans ce cas, on peut rajouter des variables pour expliquer la présence du zèbre, comme le type de végétation ou encore la présence de prédateurs. En théorie, on peut toujours rajouter autant de variables qu’on veut dans un modèle. Par contre, si on se sert de données réelles pour ajuster notre modèle (comme on l’a fait ici), il faut avoir suffisamment de données pour être sûrs que le modèle s’ajuste bien à la réalité... Et c’est une des limitations majeures en écologie. En effet, il est très coûteux de récolter beaucoup de données sur tout un ensemble de variables différentes.
Cet exemple permet d'entrevoir l'une des difficultés importantes pour étudier des systèmes écologiques : les espèces vivantes sont toutes prises dans un réseau de dépendance complexe. Par exemple, les zèbres dépendent des végétaux pour se nourrir, et les zèbres sont eux-mêmes mangés par les lions (voir l’article du Projet Pangolin sur la biodiversité). Pour bien comprendre les systèmes écologiques, il faudrait donc pouvoir étudier toutes ces relations : mais cela est très difficile, justement parce que tout est lié [5].
Cette complexité rend l’utilisation des statistiques indispensable. En effet, dès qu’on néglige une partie des facteurs, on va avoir des écarts du modèle par rapport à la réalité, et les statistiques sont nécessaires pour les prendre en compte.
Souvent, on se sert de données réelles pour construire un modèle, mais ce n’est pas pour ça que le modèle représente fidèlement la réalité [1]. En effet, les modèles expriment les hypothèses de la personne qui modélise sur le fonctionnement du monde. Cette personne s’intéresse uniquement à une partie d’un système : elle sélectionne donc les facteurs qui pourraient influencer cet aspect particulier du système.
Mais le choix de ces facteurs n'est pas facile. D’abord, il est pratiquement impossible de déterminer l’intégralité des facteurs qui influencent des phénomènes complexes (comme les systèmes écologiques). D'autre part, évaluer l’effet de certains facteurs dans la réalité peut s’avérer très difficile en pratique. Par exemple, pour le modèle de choix d’habitat du zèbre décrit précédemment, on s’intéresse à un écosystème très vaste. C'est donc difficile d’observer la répartition précise de tous les prédateurs, ou encore la végétation en tous points dans la savane... Même si le modèle essaie de décrire la réalité, il ne peut donc pas être considéré comme la réalité.
Une fois le modèle construit, il est donc crucial de le re-comparer à la réalité [5]. Pour des modèles mathématiques par exemple, on peut évaluer leur qualité en calculant la vraisemblance du modèle, c’est-à-dire une mesure de la probabilité d’obtenir les données observées avec un modèle. Plus le modèle donne des valeurs proches des données, plus il est vraisemblable. On peut aussi faire des prédictions grâce au modèle et les comparer ensuite à la réalité. Par exemple, si un modèle indique que les chauves-souris préfèrent survoler les haies pour se déplacer, on peut aller vérifier sur le terrain. Si le modèle est en accord avec la réalité, on peut avoir confiance dans ce modèle (sans oublier qu’il ne représente qu’une hypothèse sur la réalité).
Pour résumer, les modèles sont des outils qui permettent de décrire, comprendre ou prédire un phénomène. Même s’ils ne sont pas parfaits, les modèles sont néanmoins extrêmement utiles et importants en sciences.
En écologie, modéliser les écosystèmes permet de mieux les comprendre ou de mieux prédire leur évolution. Or, cela s’annonce primordial pour les années qui viennent, car les extinctions d’espèces et le changement climatique vont grandement modifier et mettre en danger le fonctionnement des écosystèmes. Pour les protéger, il faut pouvoir les comprendre et prévoir leur évolution, et les modèles sont l’un des outils indispensables pour y arriver.
Temps de travail cumulé : 33 heures
Autrice : Lisa Nicvert
[1] A. Franc, Mathématisation et modélisation, entre histoire et diversité. Editions Matériologiques, 2013, p. 974. Consulté le : 23 mars 2022. [En ligne]. Disponible sur : https://hal.inrae.fr/hal-02806211
[2] R. Frigg et S. Hartmann, « Models in Science », in The Stanford Encyclopedia of Philosophy, Spring 2020., E. N. Zalta, Éd. Metaphysics Research Lab, Stanford University, 2020. Consulté le : 23 mars 2022. [En ligne]. Disponible sur : https://plato.stanford.edu/archives/spr2020/entries/models-science/
[3] Hygiène Mentale, Ep20 Les deux vitesses de la pensée, et le « Bullshitomètre », (23 octobre 2017). Consulté le : 23 mars 2022. [Vidéo en ligne]. Disponible sur : https://www.youtube.com/watch?v=eLLIm-GpJh4
[4] J. H. Lawton, « Are There General Laws in Ecology? », Oikos, vol. 84, no 2, p. 177‑192, 1999. https://doi.org/10.2307/3546712.
[5] J.-M. Legay, L’Expérience et le modèle. Paris: INRA, 1997. Consulté le : 23 mars 2022. [En ligne]. Disponible sur : http://www.cairn.info/l-experience-et-le-modele--9782738007780-page-9.htm
[6] A. Muhlbauer, P. Spichtinger, et U. Lohmann, « Application and Comparison of Robust Linear Regression Methods for Trend Estimation », Journal of Applied Meteorology and Climatology, vol. 48, no 9, p. 1961‑1970, sept. 2009. https://doi.org/10.1175/2009JAMC1851.1.
[7] F. Varenne, Modèles et simulations dans l’enquête scientifique : variétés traditionnelles et mutations contemporaines. Editions Matériologiques, 2013, p. 11. Consulté le : 23 mars 2022. [En ligne]. Disponible sur : https://halshs.archives-ouvertes.fr/halshs-03080674
[8] L. Viollat et N. Dubois, Quand mathématiques et écosystème se marient: L’ECOLOGIE, (6 avril 2022). Consulté le : 9 avril 2022. [Vidéo en ligne]. Disponible sur : https://www.youtube.com/watch?v=iayRpCYN7Yc
[9] « Loi de Hooke », Wikipédia. 4 mars 2022. Consulté le : 9 avril 2022. [En ligne]. Disponible sur : https://fr.wikipedia.org/w/index.php?title=Loi_de_Hooke&oldid=191597667
[10] « Modèle atomique de Rutherford », Wikipédia. 20 mars 2022. Consulté le : 9 avril 2022. [En ligne]. Disponible sur : https://fr.wikipedia.org/w/index.php?title=Mod%C3%A8le_atomique_de_Rutherford&oldid=192067295
[11] « Héritabilité », Wikipédia. 26 mars 2022. Consulté le : 9 avril 2022. [En ligne]. Disponible sur : https://fr.wikipedia.org/w/index.php?title=H%C3%A9ritabilit%C3%A9&oldid=192246474
